failed start
As my first step in starting this project I picked one paper:
super-resolution from multiple images having arbitrary mutual motion - zomet, peleg
-http://www.cs.huji.ac.il/~peleg/papers/supres-book.pdf
At first look this paper was promising as a basis for an algorithm. It had simple concise mathematical equations that made a lot of sense for the super-resolution step, and a straight forward explanation of the ideas behind their super-resolution algorithm. They use a model based algorithm which is basically as follows:
Low resolution images are the result of projecting a high resolution image onto a plane, then sampling.
The goal is to use these low resolution images to find a high resolution image to fit this model.
The actual formulation of the super resolution algorithm was as a large sparse optimization problem. First a form of steepest decent was talked about, then a more effective conjugant gradient method was discussed. Here is the basic formulation:
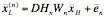
-xL is the nth low resolution image reordered as a vector.
-xH is the high resolution image reordered as a vector.
-Wn is the geometric warp matrix.
-Hn is the blurring matrix.
-D is the decimation matrix.
Then the solution could be found by minimizing
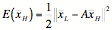
where A = DHnWn
Unfortunately much of the details that seemed clear in concept where hidden in this paper. Things such as the Wn geometric warp matrix where side stepped by saying that they were beyond the scope of the paper, which was really focused on the conjugant gradient portion of the super resolution algorithm.
I have begun following up on two of the papers that where referenced in the geometric transformation section:
“True multi-image alignment and its application to mosaicing and lens distortion correction” by H.S. Sawhney and R. Kumar
“Multi-Frame Estimation of Planar Motion” by L Zelnik-Manor and M. Irani
super-resolution from multiple images having arbitrary mutual motion - zomet, peleg
-http://www.cs.huji.ac.il/~peleg/papers/supres-book.pdf
At first look this paper was promising as a basis for an algorithm. It had simple concise mathematical equations that made a lot of sense for the super-resolution step, and a straight forward explanation of the ideas behind their super-resolution algorithm. They use a model based algorithm which is basically as follows:
Low resolution images are the result of projecting a high resolution image onto a plane, then sampling.
The goal is to use these low resolution images to find a high resolution image to fit this model.
The actual formulation of the super resolution algorithm was as a large sparse optimization problem. First a form of steepest decent was talked about, then a more effective conjugant gradient method was discussed. Here is the basic formulation:
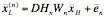
-xL is the nth low resolution image reordered as a vector.
-xH is the high resolution image reordered as a vector.
-Wn is the geometric warp matrix.
-Hn is the blurring matrix.
-D is the decimation matrix.
Then the solution could be found by minimizing
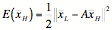
where A = DHnWn
Unfortunately much of the details that seemed clear in concept where hidden in this paper. Things such as the Wn geometric warp matrix where side stepped by saying that they were beyond the scope of the paper, which was really focused on the conjugant gradient portion of the super resolution algorithm.
I have begun following up on two of the papers that where referenced in the geometric transformation section:
“True multi-image alignment and its application to mosaicing and lens distortion correction” by H.S. Sawhney and R. Kumar
“Multi-Frame Estimation of Planar Motion” by L Zelnik-Manor and M. Irani

0 Comments:
Post a Comment
<< Home